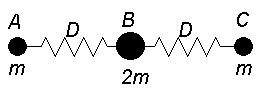
Drei
Massen sind wie in der Abbildung über Federn miteinander gekoppelt.
Eine longitudinale Normalschwingung hat die Frequenz:
|
Drei
Massen sind wie in der Abbildung über Federn miteinander gekoppelt.
Eine longitudinale Normalschwingung hat die Frequenz:
|

|
Dies gilt, wenn: