Bisher wurde die Mechanik punktförmiger Massen behandelt.
Wir wollen jetzt räumlich ausgedehnte Körper behandeln.
a) Dichte
Modellvorstellung:
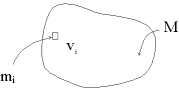
Körper mit Masse M, Volumen V
Eingeteilt in Massenelemente mi, mit Volumen Vi
 |
Anwendung (z.B. !):
Berechnung der Masse M:
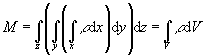
![]()
(falls ![]() räumlich konstant)
räumlich konstant)
b) Massenschwerpunkt (s. früher)

![]()
![]()
(falls ![]() konstant!)
konstant!)
Drehbewegungen
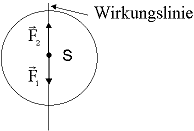
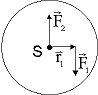
Krafteinwirkung auf ausgedehnte starre Körper bewirkt:
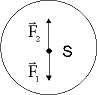
b) ![]() oder
oder ![]() wird entlang der Wirkungslinie der Kraft verschoben
wird entlang der Wirkungslinie der Kraft verschoben
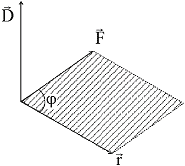 |
Vektorprodukt
|
Wirken auf einen Körper mehrere Drehmomente, so addieren sie sich vektoriell
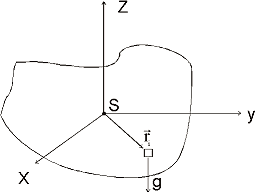
Drehachsen durch den Schwerpunkt S sind besonders ausgezeichnet:
![]()
![]() ->
-> ![]()
![]() ! (
! (![]() )
)
Ein Körper ist stabil (keine Drehung!) wenn er drehbar um eine
Achse durch den Schwerpunkt S gelagert ist (![]() )
)
=>
Anwendungen:
1. Experiment
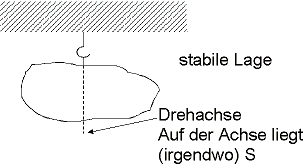
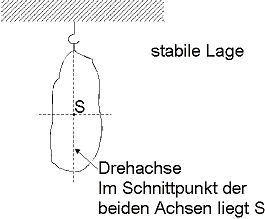
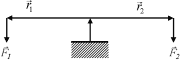
c) Einarmiger Hebel
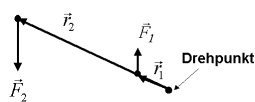
d)
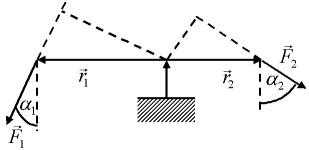
3.6.2. Trägheitsmoment / Rotationsenergie
| Translation | Rotation |
| m | I |
| v |
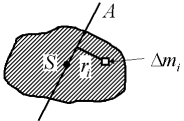
Impuls des Massenelementes (siehe Zeichnung!)
![]()
Definition: Drehimpuls
![]()
![]()
=> ![]()
Einheit: ![]()
=> ![]()
![]() ist ein axialer
Vektor
ist ein axialer
Vektor
Wenn eine Kraft ![]() auf
auf ![]() wirkt mit
wirkt mit ![]() dann dreht sich der Körper.
dann dreht sich der Körper.
Es wirkt das Drehmoment D:
![]()
![]()
Allgemein: ![]()
Wenn ![]() dann folgt
dann folgt ![]()
Drehimpulserhaltungssatz
Der gesamte Drehimpuls eines Körpers (System von Teilchen) bleibt
konstant wenn kein äußeres Drehmoment auf ihn wirkt.
![]() z. B., wenn
z. B., wenn ![]()
oder ![]() parallel zu
parallel zu ![]()
(Zentralkräfte)
Anwendungsbeispiele: Experimente zum Drehimpulserhaltungssatz
Wirkt ein Drehmoment ![]() auf einen Körper, so gilt:
auf einen Körper, so gilt:
![]()
![]() bewirkt eine
Winkelbeschleunigung
bewirkt eine
Winkelbeschleunigung ![]()
(Analog: Translation ![]() )
)
Ist ![]() ,
, ![]()
=> ![]()
![]()
(Hinweis: Analog zur Translation)
3.6.4 Berechnung von Trägheitsmomenten
Bisher: Berechnung von Trägheitsmomen-ten bezüglich Achsen
durch den Schwer-punkt.
Wie groß ist IB bezüglich Achse
B parallel zu A?
Körper von oben betrachtet
![]()
![]()
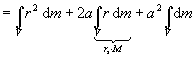
rs = 0 (Koordinatenursprung ist Schwerpunkt)
![]()
Steiner´scher Satz:
| Das Trägheitsmoment eines Körpers bei Rotation um beliebige Achse B ist gleich dem Trägheitsmoment des Körpers um eine zu B parallele Achse durch den Schwerpunkt plus das Trägheitsmoment der im Schwer-punkt vereinigten Masse bezüglich B. |
Einfache Beispiele zur Berechnung von Trägheitsmomenten:
a) Zweiatomiges Molekül
![]()
Umrechung:
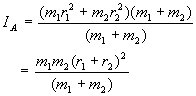
![]()
![]() "reduzierte
Masse"
"reduzierte
Masse"
entspricht dem Trägheitsmoment der reduzierten Masse im Abstand ![]() vom Schwerpunkt
vom Schwerpunkt
Hinweis 1: Trägheitsmoment bezüglich einer Drehachse durch
die Molekül-achse ist sehr klein!
Hinweis 2: Man kann Molekülrotationen beobachten mit "Rotationsspektren"
Daraus kann I direkt gemessen und die Molekülstruktur bestimmt
werden.
b) Hohlzylinder
![]()
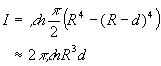
![]()
Vollzylinder:
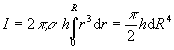
![]()
3.6.5. Hauptträgheitsachsen
Starre Körper, Massenelement ![]()
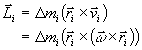
![]()
(Vektorrechnung: 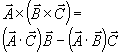 )
)
=> ![]()
=> ![]()
![]() Trägheitstensor
Trägheitstensor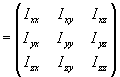
Trägheitstensor ist "diagonalisierbar", d. h.
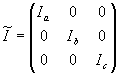
mit ![]() (Hauptträgheitsmomente)
(Hauptträgheitsmomente)
Körper rotiert "frei" um Achsen mit Hauptträgheitsmomenten
Stabile Achsen für das größte und kleinste Trägheitsmoment
3.6.6. Vergleich: Rotation
- Translation
| Rotation | Translation |
| Winkel: |
Weg: |
| Trägheitsmoment: I | Masse: m |
| Winkelgeschwindigkeit: |
Geschwindigkeit |
| Drehimpuls: |
Impuls |
| Drehmoment: |
Kraft: |
3.6.7 Kreiselpräzession
Ein äußeres Drehmoment wirkt auf einen Kreisel:
![]()
z. B.: Kreisel wird nicht im Schwerpunkt unterstützt
=> ![]()
(![]() : Abstand zwischen Schwerpunkt
und Unterstützungspunkt)
: Abstand zwischen Schwerpunkt
und Unterstützungspunkt)
ist ![]()
![]() bewirkt eine Änderung
der Richtung von
bewirkt eine Änderung
der Richtung von ![]()
![]()
![]()
Kreiselachse weicht ![]() senkrecht aus!
senkrecht aus!
![]()