3.8. Gravitation und Planetenbewegungen

a) Gravitationsgesetz

Newtons Beobachtung des freien Falls und der Planetenbewegungen führt zum Gravitationsgesetz:
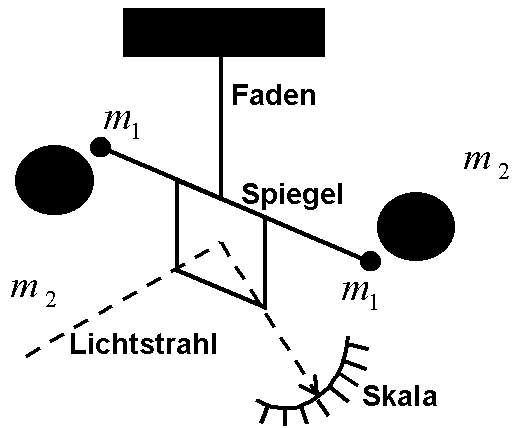
2 Massen ziehen sich gegenseitig an (m1, m2)

Abstand: r

  Anziehung m1- m2 bewirkt ein Drehmoment auf den Faden. Reflektierter Strahl bewegt sich.
r: Es gilt der Abstand zwischen den Schwerpunkten von m1, m2
Aus der Fallbeschleunigung kann die Masse der Erde mE bestimmt werden: 95.gif" HEIGHT=37 WIDTH=182>
  b) Keplersche Gesetze
 
1. Keplersches Gesetz  
Die Planeten bewegen sich auf Ellipsen, in deren einem Brennpunkt die Sonne steht. 

2. Keplersches Gesetz 
Der Radiusvektor von der Sonne zum Planeten überstreicht in gleichen Zeiten gleiche Flächen. 

3. Keplersches Gesetz 
Die Quadrate der Umlaufzeiten verhalten sich wie die dritten Potenzen ihrer großen Halbachsen. 
 
Gesetze sind empirisch (aus Beobachtungen). Sie liefern die Grundlage für Newtons Entwicklung des Gravitationsgesetzes Eine Ellipse ist die Menge der Punkte, für die die Summe ihrer Distanzen zu den beiden Brennpunkten F konstant ist. Eine solche Figur läßt sich zeichnen, wenn man eine Schnur an den beiden Brennpunkten befestigt und mit ihrer Hilfe, in der Abbildung am Punkt M gezeigt, einen Stift führt. Der Abstand a wird die große Halbachse, b die kleine Halbachse der Ellipse genannt. Wenn die beiden Brennpunkte zusammenfallen (numerische Exzentrizität ), dann sind a und b gleich, und die Ellipse ist in einen Kreis übergegangen. zum 1. Keplerschen Gesetz:
Energieerhaltung bei Planetenbewegung: => Bahnkurve (Ellipse) folgt aus Energiesatz
Ist zum 2. Keplerschen Gesetz: Vektor  steht senkrecht auf Fläche (,)

Es gilt der Drehimpulserhaltungssatz: =const, weil  Zentralkraft ist: (  => ! )
Also: 
 

Zum 3. Keplerschen Gesetz:

Gravitationskraft wirkt als Zentralkraft, also:

Anwendungen

a) "Erde wiegen"

  =>  = 5,84 1024 kg
  b) "Sonne wiegen"
Bestimmung der Konstante  (aus Planetenbahnen und Umlaufzeiten)
=> MS = 3,33 105 mE
 

c) "Planeten wiegen"

Bestimmung der Umlaufdauer von Monden um Planeten
Bestimmung des Bahnradius von Monden und Planeten

Beispiel: Jupitermond Io
Bahnradius: r = 4,22 103 km
Umlaufzeit: T = 1,5 105 s
=> MJupiter= 330 mE

d) Satelliten

Wie groß ist die Fallbeschleunigung in einem Satelliten in 200 km Höhe über der Erde?

Warum sind Astronauten "schwerelos"? Mikrogravitation?
Nein, sondern Kräftefreiheit: (= Fliehkraft) Die Kräfte heben sich auf, wenn eine stationäre Bahn erreicht ist.
 

e) Geostationäre Bahn

Umlaufzeit: T = 24 h
aus 
=> Bahnradius 
 

f) Effektives Potential

Annahme: Planetenbewegung ist Kreisbahn
Potential durch Gravitation:

Energie durch Rotation: 
Die Summe der Energien stellt das effektive Potential dar, in dem sich der Planet bewegen kann 1) Bewegung in dem "Topf" sind "gebundene" Bewegungen
2) Bewegungen mit Eges > 0 sind "ungebunden". Körper kann nach "Unendlich" gelangen.
 

Einige Abschlußbemerkungen zur "Gravitation und Planetenbewegungen"
1  Die Lage der Planetenebenen ist abhängig von den Anfangsbedingungen bei der Planetenentstehung (rotierende Gaswolken). Bezüglich der Bahnebene der Erde sind die anderen Ebenen der Planeten-bewegungen um ca. 0°-15° geneigt. 
2 Die Kraft unter der sich die Planetenbewegungen vollzieht ist nur näherungsweise eine Zentralkraft! (Einflüsse von Planeten!) 
3 Einige Planetenbahnen sind näherungsweise Kreise (Exzentrizitäten: 0.05 – 0.2, Erde: 0.017) 
4 Die Sonne liegt nicht exakt im Brennpunkt einer Ellipse. Das Sonne/Planetensystem bewegt sich um den gemeinsamen Schwerpunkt. Dieser liegt innerhalb der Sonne. .... weiteres dazu in der Vorlesung "Astronomie"