Drehachse: Gerade durch Z senkrecht zur Bahnebene
Fahrstrahl: Vektor
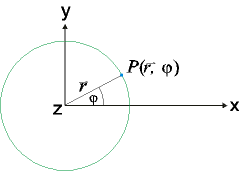
Lage des Massenpunktes (am günstigsten) mit Polarkoordinaten beschreiben: (r,
Beispiel einer zweidimensionalen (krummlinigen) Bewegung
Massenpunkt bewegt sich auf einer Kreislinie um das Drehzentrum Z
Drehachse: Gerade durch Z senkrecht zur Bahnebene
Fahrstrahl: Vektor ![]() von Z zum Ort P des Massenpunktes
von Z zum Ort P des Massenpunktes
Lage des Massenpunktes (am günstigsten) mit Polarkoordinaten beschreiben:
(r,![]() )
)
 |
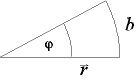 |
| Radius: r
Winkel: |
Winkel in Bogenmaß gemessen:
Bogenmaß = |
Bahngeschwindigkeit: ![]()
Winkelgeschwindigkeit: ![]()
![]()
Einheit der Winkelgeschwindigkeit: rad s-1
![]() ist ein axialer Vektor:
ist ein axialer Vektor:
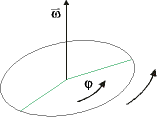 Drehrichtung
Drehrichtung
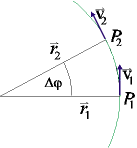
Kreisbewegung mit konstanter Bahngeschwindigkeit:
| v = const ; |
 |
|
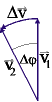 |
Beschleunigung: ![]()
b heißt Zentripetalbeschleunigung
b zeigt stets zum Kreismittelpunkt Z (in Richtung von ![]() )
)
Mit v = r![]() erhält man:
erhält man:
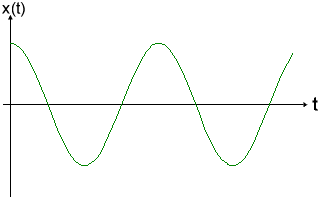
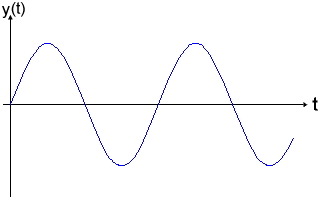
Beschleunigung: ![]()