Arbeit

Verschiebt eine Kraft F einen Körper um eine Wegstrecke ds, so verrichtet sie mechanische Arbeit dW, mit:
dW =  (Skalarprodukt!)
Die Arbeit ist ein Skalar!
Einheit der Arbeit: 1 Nm = 1 kg× m²s^-2 = 1 J (Joule)
Allgemein gilt für die Gesamtarbeit beim Verschieben um eine Wegstrecke zwischen zwei Punkten 1, 2:

Linienintegral 

(Bemerkung: Stehen  und  senkrecht aufeinander, so ist W = 0! Siehe skalares Produkt zweier Vektoren)

Leistung

Die Arbeit, die pro Zeitintervall verrichtet wird nennt man Leistung:
     (falls zeitunabhängig ist)

Die Leistung ist ein Skalar!
Einheit der Leistung: 1 J/s = 1 W (Watt)
(Früher: andere Einheit der Leistung: 1 PS = 735,5 W)

Beispiele:

meschliche Leistung (Spitze!)	1 kW
meschliche Leistung (Durchschnitt)	100 W
Hörsaalbeleutung	4 kW
Kernkraftwerk	ca. 1200 MW

 

Wegunabhängige Arbeit

Es gibt Kraftfelder, für die gilt, daß die Arbeit W für beliebige Wege zwischen zwei Punkten im Raum
gleich groß ist, also:

In diesem Fall ist das Wegintegral längs eines geschlossenen Weges 0:

Kräfte, für die das Integral W wegunabhängig sind, heißen "konservativ"
(trifft nur zu für zeitunabhängige Kräfte)

Die Arbeit W hängt nur vom Anfangs- und Endpunkt ab!
 

Potentielle Energie

In einem konservativen Kraftfeld hängt die Arbeit, einen Körper von einem Punkt x_o zum Punkt x zu bringen nur von der Lage von x ab:

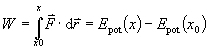
E_pot(x) wird mit "potentieller Energie" bezeichnet (Energie der Lage).

Der Körper kann diese Energie in Arbeit verwandeln
Nullpunkt der potentiellen Energie:
- im Ursprung des Koordinatensystems
oder
- im Unendlichen

Vorzeichenkonvention:
Arbeit bei Bewegung gegen eine Kraft ist negativ (dem Körper muß Energie zugeführt werden)

Potentielle Energie: 3 Beispiele 

a)	Hubarbeit
	Körper gegen Schwerkraft anheben
b)	Elastische Arbeit
	Fx = D x     W = ½ D x2   Elastische (Feder-) Energie
c)	Energie in einem Zentralkraftfeld
	Annahme: anziehendes Kraftfeld  (siehe später Gravitationsfeld)  mit

 

Kinetische Energie

Die kinetische Energie ist die Energie der Bewegung, die in dem Körper steckt, der sich mit der Geschwindigkeit v bewegt:

Ausgehend von:
F = m dv/dt und v = ds/dt
Gilt: dW = F ds = m · dv/dt v dt = mv·dv

Integration: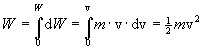 

(kinetische Energie)
 
 

Energiesatz der Mechanik

Die Summe aller mechanischen Energien in einem abgeschlossenen System ist konstant:

    E_pot + E_kin + E_elast. = E _gesamt = const

Gilt für konservative Kräfte!

Der Energieerhaltungssatz soll an vier Beispielen erläutert werden:

a) Elastischer Gummiball  Ein Gummiball (Masse m) fällt von der Höhe h auf den Boden, wird dort reflektiert und erreicht wieder die Höhe h.  Epot + Ekin + Eelast. = const      Zu Beginn (1)  Epot = mgh = E gesamt Ekin = 0, Eelast. = 0 Kurz vor dem Aufprall am Boden (2) Ekin = mv2/2 = E gesamt  Epot = 0, Eelast. = 0  Nach dem Aufprall wird der Ball  elastisch verformt (Federkraft D, Verformung: x) (3) E elast = ½ Dx2 = E gesamt  Epot = 0, Ekin = 0  Nach der Entspannung fliegt der Ball nach oben (4) Ekin = mv2/2 = E gesamt Epot = 0, Eelast. = 0  Nach der Rückkehr zur Höhe h: Epot = mgh = E gesamt Ekin = 0, Eelast. = 0 Bei diesem Vorgang werden (periodisch) potentielle Energie in kinetische Energie und elastische Energie umgewandelt. Die Gesamtenergie bleibt konstant.  Wir können berechnen:  Aufprallgeschwindigkeit aus:  mgh = mv2/2    (unabhängig von der Masse! Warum?)  Verformung x aus:

b) Federpendel   Eine Masse m wird an eine Feder (Federkonstante D) gehängt und ausgelenkt. Das System Feder-Masse schwingt.    Periodisch wird elastische Energie in kinetische Energie umgewandelt. Die Gesamtenergie bleibt konstant.  Aus einer Energiebilanz läßt sich die Bewegungsgleichung x(t) der schwingenden Masse berechnen:    Die Gleichung wird nach der Zeit t abgeleitet (Übung!), wobei dEges/dt = 0 !  Ergebnis:   (Dieses Ergebnis erhält man auch, wenn man nur die Kräfte in einer Bilanzgleichung betrachtet)  Die Lösung dieser Differentialgleichung lautet:               Durch Anfangsbedingungen  z.B.: x(t = 0) = A = x0

c) Fadenpendel  An einem Faden der Länge l hängt eine Masse m. Die Masse wird aus der Ruhelage ausgelenkt. Danach schwingt das Pendel periodisch um die Ruhelage.  Aus einer Energiebilanz läßt sich die Bewegungsgleichung berechnen:           =>    Unter der Annahme kleiner Auslenkwinkel:  (Näherung)  erhalten wir      siehe Abschnitt b)    oder der Schwingungsdauer des Fadenpendels  (unabhängig von m!  Möglichkeit zur Messung von g!)  Nebenbemerkung:  Mit wachsender Amplitude A steigt T an!  Näherung nicht mehr richtig!

d) Raketenschuß  Eine Masse m (Rakete) soll aus dem Einzugsbereich der Erse (Masse mE, Radius rE) hinausgeschossen wreden. Wie groß ist die "Fluchtgeschwindigkeit"?  Sehr vereinfachte Annahmen:  m , mE sind Massenpunkte  g : Fallbeschleunigung ist konstant  Weit weg von der Erde ist Gesamtenergie 0!    v0: Anfangsgeschwindigkeit der Rakete    mit g = 10   rE = 6370 km  v0 = 11,3     Nebenbemerkung:  Um einen 70 kg-Menschen in den Weltrum zu schießen brauchen wir die Energie:    Bei einem Preis von 10 Pfg pro kWh sind dies Kosten von 125 DM! Wo liegt der Fehler?

 

Weitere Anwendungen des Energieerhaltungssatzes

Einfache Maschinen
Beispiele: schiefe Ebene, Hebel, Flaschenzug
Mit  (= const) gilt:

Durch Vergrößerung des Weges genügt bei gleicher Arbeit eine geringere Kraft zur Durchführung der Aufgabe
 
 
 

a)	Schiefe Ebene  Masse m soll auf Höhe h angehoben werden    1  W = mgh => F1 = mg (Weg = h)  2 W = mgh => F2 = mg  F2 < F1 und Weg2 > Weg1
b)	Flaschenzug      Fg = mg auf 4 Seilenstücke verteilt  Fz = Fg  Um m die Strecke s1 zu heben, müssen 4 Seilstücke um s1 verkürzt werden  sz = 4 s1 und Fg s1 = Fz sz