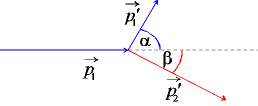
Anwendung des Energie-, Impulserhaltungssatzes
2 Teilchen m1, m2
Annahme: 1 Teilchen ruht vor dem Stoß

![]()
![]()
Q = 0 elastischer Stoß
Q < 0 inelastischer Stoß
Q > 0 superelastischer Stoß
Annahme: elastischer Stoß
(1) ![]() =
=![]() +
+![]() (
(![]() =0, Teilchen 2
ruht)
=0, Teilchen 2
ruht)
(2) ![]() =
= ![]() +
+ ![]()
Lösung graphisch darstellbar:
Aus (1), (2) folgt 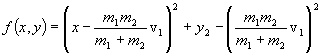
(Kreisrelation)
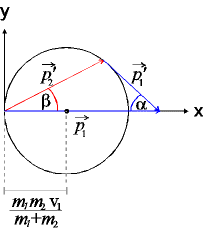
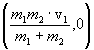
Radius: ![]()
Auf der Kreislinie treffen sich alle möglichen Lösungen ![]() +
+![]() (d.h. Spitze des Vektors
(d.h. Spitze des Vektors ![]() liegt immer auf Kreislinie)
liegt immer auf Kreislinie)
Spezialfälle
a) Zentraler Stoß:
![]() ,
,![]() ,
,![]() parallel zueinander
parallel zueinander
| (1), (2) => | |
b) Nichtzentraler Stoß und m1 = m2
= m
| (1), (2) => | ||
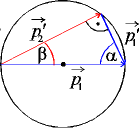 |
c) Nichtzentraler Stoß und m1 << m2
| (1), (2) => | |
Stoßprozesse lassen sich leichter im "Schwerpunktsystem" beschreiben
Massenschwerpunkt
Gegeben sind N Teilchen mit ![]() ,
, ![]()
Definition des Massenschwerpunktes:
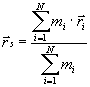
=> ![]()
Der Impuls des Massenpunktes ist gleich der Summe der Einzelimpulse
=> Der Impuls des Massenschwerpunktes eines abgeschlossenen Systems ist konstant, d. h. seine Geschwinigkeit ändert sich nicht.
Aber:
Ist ![]()
Der Schwerpunkt bewegt sich so, als ob er ein Körper mit Gesamtmasse ![]() wäre und auf ihn die äußere Kraft
wäre und auf ihn die äußere Kraft ![]() wirke.
wirke.
(Hinweis: Rechtfertigung für "Punktmechanik")
Schwerpunktsystem
Teilchen im Laborsystem: Ortsvektoren ![]()
Schwerpunktsystem: "Ursprung" ist Schwerpunkt (![]() )
)
Ortsvektoren: ![]()
![]()
mit: 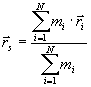
![]()
Differentiation nach Zeit t
![]()
| Summe aller Impulse im Schwerpunktsystem ist immer Null! |
Energie?
2 Teilchen
![]()
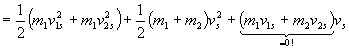
=> ![]()
| Kinetische Energie im Laborsystem ist gleich der Summe der Kinetischen Ener-gien im Schwerpunktsystem und der kinetischen Energie der im Schwerpunkt vereinigten Gesamtmasse |
Schlußfolgerungen für Stöße zwischen Teilchen:
Berechnungen im Schwerpunktsystem!
2 Teilchen:
Vor Stoß:
![]()
![]()
Nach Stoß:
![]()
![]()
Schwerpunktsystem:
![]()
![]()
=> für elastischer Stoß
im Schwerpunktsystem:
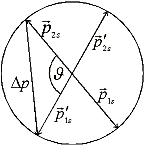
Impulsübertrag
![]()
maximal für ![]()
![]()
Laborsystem:
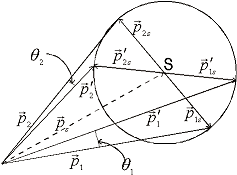
Hinweis:
Newton-Diagramme
Darstellung der Geschwindigkeiten (nicht Impulse) im Schwerpunkt- und
Laborsystem!