4 Schwingungen und
Wellen
Bedeutung für:
-
Akustik (Schallquellen, Empfänger, Ausbreitung)
-
Mechanik von Festkörpern, Materialwissenschaften
-
Gemeinsamkeiten von mechanischen und elektromagnetischen Schwingungen/Wellen
-
Untersuchung von Gasen, Flüssigkeiten, Festkörpern, Molekülen,
... mittels "Schwingungs-Spektroskopie"
-
...
4.1 Freie Schwingungen
Bereits besprochen wurde das Fadenpendel, Federpendel:
Fadenpendel:
Differentialgleichung:
Bemerkungen:
1) Schwingungsfrequenz  unabhängig von Amplitude, Masse
unabhängig von Amplitude, Masse
2)  wird bei größeren
Amplituden auch amplitudenabhängig!
wird bei größeren
Amplituden auch amplitudenabhängig!
3) Fadenpendel geeignet zur Bestimmung von g!
4.1.1 Freie ungedämpfte
Schwingung
am Beispiel der Federschwingung
Rücktreibende Kraft: 
Trägheitskraft: 
=> 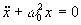
 Ergebnis:
Ergebnis: 
"harmonischer Oszillator" (nur eine Frequenz)
 durch Anfangsbedingungen
festgelegt
durch Anfangsbedingungen
festgelegt
 unabhängig
von Amplitude!
unabhängig
von Amplitude!
 Schwingungsdauer
[s]
Schwingungsdauer
[s]
 Frequenz [Hz]
Frequenz [Hz]
Eges = Ekin + Epot
= ½ Dx2 + ½ mv = const
=> Eges = ½ Dx02
Energie proportional zum Quadrat der Amplitude!
 Federschwingung ist ein "gutes" Modell für viele physikalische Überlegungen:
Federschwingung ist ein "gutes" Modell für viele physikalische Überlegungen:
-
Molekülschwingungen
-
Schwingungen von Festkörpern, etc
i. A. ist die Energie aber nicht: E ~ x02
Aber "in guter Näherung" gilt in der Nähe des Gleichgewichts:
E ~ x02
In der Nähe der Gleichgewichtslage ist Schwingung "harmonisch"
4.1.2 Freie gedämpfte
Schwingung
Annahme: Reibungskraft ~ Gewichtskraft
(siehe Stoke´sche Reibung)


Lösungsansatz:

Einsetzen:
=> 
=> 
=> 
Diskussion dieser Lösung:
Offensichtlich erhält man mathematisch unterschiedliche Lösungen
wenn  ist
ist
a) "Schwache Dämpfung"
 Substitution:
Substitution: 

Ergebnis ist gedämpfte Schwingung (nicht harmonisch)
Frequenz  ist kleiner als
ist kleiner als  !
!
Frequenzverschiebung wächst mit der Dämpfung!

b) "Starke Dämpfung"

Substitution:  =>
=> 

Keine Schwingung („kriechen“)
c) "Aperiodischer Grenzfall"
 =>
=> 

d) Quantitative Beschreibung der Dämpfung
Die Schwingung verliert Energie:
Leistung 
Güte der Schwingung:
Definition: Q- Wert (relativer Energieverlust pro Schwingungsperiode)
Dämpfung wird in Dezibel angegeben:
Anfangsenergie: E1
Endenergie: E2
Def:  weil E ~ Amplitude A2
weil E ~ Amplitude A2
Def: => 
Bsp: Keine Dämpfung A1= A2
=> a = 0 dB
Dämpfung A1= 10 A2
=> a = 20 dB
Dämpfung A1= 1000 A2 => a
= 60 dB



![]()

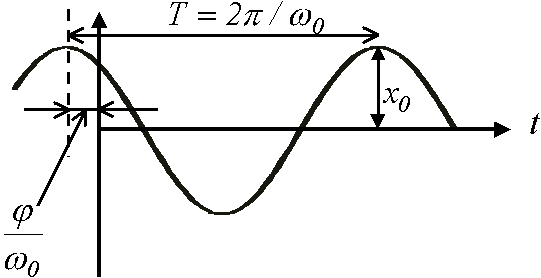
![]() Frequenz [Hz]
Frequenz [Hz]

![]() gegen x um ½
gegen x um ½![]() phasenverschoben
phasenverschoben
![]() gegen x um
gegen x um ![]() phasenverschoben
phasenverschoben


![]()

![]()
![]()
![]()
![]()
![]() ist
ist
![]() Substitution:
Substitution: ![]()

![]() ist kleiner als
ist kleiner als ![]() !
!

![]()
![]() =>
=> ![]()
![]()

![]() =>
=> ![]()
![]()

![]()
![]() weil E ~ Amplitude A2
weil E ~ Amplitude A2
![]()