1.3 Thermische Ausdehnung

1.3.1 Thermische Ausdehnung von Festkörpern und Flüssigkeiten

Bei fast allen Festkörpern beobachtet man eine Ausdehnung mit steigender Temperatur. In einem beschränkten Temperaturbereich kann man die Längenänderung beispielsweise eines Metallstabs proportional zur Temperatur annehmen:

lineare Ausdehnung

L gibt dabei die Länge des Stabs an. wird als linearer Ausdehnungskoeffizient bezeichnet, der – materialabhängig – die relative Längenänderung pro Grad Temperaturänderung angibt:

linearer Ausdehnungskoeffizient

Für die meisten Stoffe gilt , d.h. sie dehnen sich mit steigender Temperatur aus. Genauere Messungen ergeben auch für eine Temperaturabhängigkeit:

Festkörper dehnen sich bekanntlich nicht nur in einer Raumrichtung aus, sondern auch im Volumen. Allgemein gilt für die Volumenausdehnung nichtisotroper Stoffe:

Mit dem Volumen V₀ bei 0°C und gilt

Volumenausdehnung

Die Ausdehnung nichtisotroper Stoffe kann in allen drei Raumrichtungen unterschiedlich groß sein. Im Fall homogener, isotroper Körper ist sie in allen Richtungen gleich und die Gleichung vereinfacht sich:

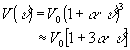für

mit

Für Flüssigkeiten lässt sich sinnvollerweise nur der Volumenausdehnungskoeffizient angeben. Dieser ist aber im Allgemeinen wesentlich größer als der Volumenausdehnungskoeffizient von Metallen.

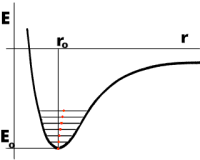Anharmonisches Wechselwirkungs-potenzial zwischen Atomen in einem Festkörper. Der mittlere Abstand (rote Punkte) wächst mit steigender Energie und damit steigender Temperatur.

Physikalischer Hintergrund

Zum Verständnis⁵ der thermischen Ausdehnung muss man das unsymmetrische Wechselwirkungspotenzial zwischen den Atomen eines Festkörpers betrachten. Die Atome in einem Festkörper schwingen aufgrund der thermischen Energie in der Potenzialmulde hin und her.

Mit zunehmender Temperatur steigen kinetische und potenzielle Energie der Atome. Der Schwingungsmittelpunkt wandert aufgrund des anharmonischen Potenzials nach rechts zu größeren mittleren Abständen der Atome. Das Material dehnt sich aus.

Experiment: Ausdehnung von Wasser beim Gefrieren

Experiment: Kugel durch Ring

Experiment: Glühender Draht

Experiment: Bolzensprenger

Experiment: Kontraktion von Gummi beim Erwärmen

⁵ vgl. auch Demtröder (1998, S. 273) oder Stierstadt (1989, S. 337)