|
Gasteilchen übertragen beim Zusammenstoß mit der Wand einen bestimmten Impuls und üben dadurch eine Kraft auf die Wand aus. Den dadurch verursachten Druck beschreibt die Grundgleichung der kinetischen Gastheorie.
 |
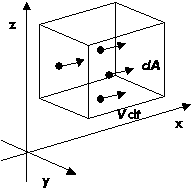| Zur Herleitung der Grundgleichung der kinetischen Gastheorie. |
Zur Herleitung9 betrachten wir zunächst
nur die Teilchen nx mit Geschwindigkeitskomponente vx
und Masse m, die sich in einem quaderförmigen Volumen 
in positiver x-Richtung bewegen. Auf das Wandelement A treffen in der
Zeit dt
Teilchen, wobei jedes Teilchen eine Impulsänderung von 
erfährt. Die Teilchen übertragen auf die Wand eine Kraft 
.
Damit ist der Druck
.
Bislang wurden nur Teilchen mit einer Geschwindigkeitskomponente vx betrachtet. Gasteilchen haben aber unterschiedliche Geschwindigkeiten und bewegen sich in allen Raumrichtungen.
Wollen wir die Gleichung verallgemeinern, müssen wir daher zum einen die
Geschwindigkeitskomponenten vy und vz berücksichtigen.
Zum anderen sind auch die Beträge der Geschwindigkeit 
nicht für alle Teilchen identisch, weshalb wir zu den mittleren Geschwindigkeitsquadraten
übergehen.
Die Geschwindigkeiten und damit der Druck in einem ruhenden Gas sind isotrop verteilt, d.h. jede Richtung ist gleichwahrscheinlich. Deshalb muss auch der Impulsübertrag in alle Richtungen gleich groß sein. Für die Mittelwerte der Geschwindigkeitsquadrate gilt dann
.
Im Mittel bewegen sich gleichviele Teilchen in +x-Richtung, wie in –x-Richtung. Der Druck, den alle Moleküle auf eine Wand in der y-z-Ebene ausüben, ist daher bei einer Teilchenzahldichte n
.
Mit 
und
der Gleichheit der Mittelwerte der Geschwindigkeitsquadrate gilt
.
Damit erhält man für den gesamten Druck
Grundgleichung der kinetischen Gastheorie.
Umformuliert lässt sie sich schreiben als
9 Herleitungen sind z.B. zu finden in Demtröder (1998, Kap. 7.3.2, S. 199 f) oder Hering (1992, S.152).
© Universität Würzburg, Tilo Hemmert 2000