4.2.2 Nicht-stationäre Wärmeleitung

Etwas komplizierter wird es im nicht-stationären Fall . Zur Herleitung beschränken wir uns auf den eindimensionalen Fall.

Wie wir gesehen haben, ist der Wärmestrom proportional zum Temperaturgefälle

Wir betrachten einen differentiell kleinen Ausschnitt aus einem wärmeleitenden Stab.

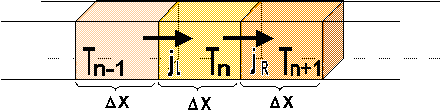Differentiell kleiner Ausschnitt aus einem wärmeleitenden Stab

Es lassen sich die Wärmeströme j_L, j_R berechnen: und

Da resultiert eine Netto-Wärmezufuhr von

.

Diese Wärmezufuhr führt zur Temperaturänderung

(c: spezifische Wärmekapazität, : Dichte).

Damit erhält man die Temperaturänderung pro Zeiteinheit:

Führt man die Betrachtung für differentiell kleine Größen durch, ergibt sich die Wärmeleitungsgleichung:

Wärmeleitungsgleichung (eindimensional)

bzw. ganz allgemein als

Wärmeleitungsgleichung (allgemein)

D_w bezeichnet man als Temperaturleitzahl, ist der Laplace-Operator.

© Universität Würzburg, Tilo Hemmert 2000