4.3.3 Planck’sches Strahlungsgesetz

"Vogelhaus" - Modell für einen schwarzen Körper / Hohlraum-strahler.

Experimentell lässt sich ein schwarzer Körper in Näherung durch einen Hohlraum realisieren, dessen Austrittsöffnung sehr klein gegen die gesamte Innenfläche ist. Strahlung, die auf die Öffnung trifft, wird im Inneren sehr oft reflektiert bevor sie die Austrittsöffnung wieder erreicht. Sie kommt praktisch nicht mehr aus dem Hohlraum heraus. Heizt man die Wände des Hohlraumes auf eine Temperatur T auf, so wirkt die Öffnung als eine Strahlungsquelle. Daher kann man einen schwarzen Körper auch als Hohlraumstrahler bezeichnen.

Die Emission eines schwarzen Körpers wird beschrieben durch die spektrale Energiedichte , die die Energie des Strahlungsfeldes pro Volumeneinheit und pro Frequenzintervall angibt.

Die Energiedichte w des Strahlungsfeldes erhält man durch Integration der spektralen Energiedichte:

Energiedichte

Die Strahlungsintensität I ist gegeben durch

Strahlungsintensität

Sie gibt die Leistung pro Flächeneinheit an. Einheit: . (c Lichtgeschwindigkeit)

Um die empirischen Ergebnisse über die Energieverteilung eines schwarzen Strahlers zu verstehen, führte Max Planck 1900 die Quantenhypothese ein.

Die Quantenhypothese besagt, dass ein strahlendes System Energie nicht beliebig mit dem Strahlungsfeld austauschen kann, sondern nur in ganzzahligen Vielfachen des Energiequantums .

Dabei ist h das Planck´sche Wirkungsquantum: .

Um einen Ausdruck für die spektrale Energiedichte zu erhalten, betrachten wir eine Gruppe von Teilchen, die Strahlung der Frequenz aufnehmen und abgeben können. Nach einem Absorptionsakt haben die nun angeregten Teilchen eine um höhere Energie, da nach der Quantenhypothese Energie nur in ganzzahligen Vielfachen von aufgenommen werden kann.

Im thermodynamischen Gleichgewicht gilt für die Zahl der angeregten Teilchen N^* und die Zahl der nicht angeregten Teilchen N₀ die Boltzmann-Verteilung:

Es gibt verschiedene Möglichkeiten für einen Energieaustausch zwischen Teilchen und Strahlung:

1. Absorption
   Teilchen absorbieren Strahlung vom Betrag . Die Zahl der Absorptionen pro Zeit- und Volumeneinheit ist proportional zur Zahl der nicht angeregten Teilchen und zur Intensität der Strahlung:
   
   p: Wahrscheinlichkeit der Absorption
2. Spontane Emission
   Teilchen emittieren Strahlung vom Betrag . Die Zahl der spontanen Emissionen pro Zeit- und Volumeneinheit hängt von der Zahl der angeregten Teilchen ab:
   
   p‘: Wahrscheinlichkeit der spontanen Emission
3. Erzwungene Emission
   Teilchen werden durch Strahlung "durchgeschüttelt" und dadurch zur Emission der gespeicherten Energie gezwungen. Die Zahl der erzwungenen Emissionen pro Zeit- und Volumeneinheit ist abhängig von der Zahl der angeregten Teilchen:
   

Im Gleichgewicht ist die Zahl der Absorptionen gleich der Zahl der Emissionen.

Nach einer komplexeren Herleitung²⁶, auf die hier nicht weiter eingegangen werden kann, erhält man das Planck´sche Strahlungsgesetz, das die spektrale Energiedichte eines schwarzen Körpers angibt:

Planck‘sches Strahlungsgesetz

Experiment: Wärmestrahlung einer Kohlenbogenlampe

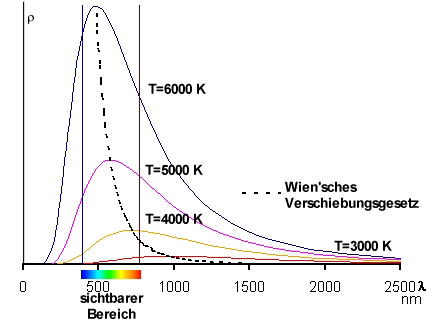Spektrale Energiedichte über der Wellenlänge aufgetragen.

Um das Maximum der spektralen Energiedichte zu erhalten, setzt man die Ableitung nach gleich Null: und erhält das Wien‘sche Verschiebungsgesetz:

Wien‘sches Verschiebungsgesetz

Zur Vertiefung

1. Auch die Sonne kann man als schwarzen Körper betrachten. Berechnen Sie die Temperatur an der Sonnenoberfläche! Sie wissen, dass die spektrale Energiedichte der Sonne im Bereich des sichtbaren Lichts bei maximal ist. (T = 6000 K)
2. Schätzen Sie die Nettostrahlungsleistung eines nackten Menschen bei Raumtemperatur (T₀ = 293 K) ab. Er sei 1,75 m groß. Nähern sie die Oberfläche des Menschen durch einen Zylinder mit einem Umfang von 0,80 m. Nehmen Sie einen idealen Emissionsgrads (e = 1) an. (P_netto = 111 W)

²⁶ Eine Herleitung ist beispielsweise zu finden in Demtröder (1999, Kap. 12.4) oder in Frauenfelder-Huber (1970, S.147f). Eine Diskussion der Grenzfälle findet man beispielsweise in Gerthsen (1993, Kap. 11.2.6)

© Universität Würzburg, Tilo Hemmert 2000