3.1.3.1 Geradlinige (eindimensionale) Bewegung
 

Die Bewegung erfolgt auf einer Geraden (z.B.: x-Achse)

Anfangsbedingung: Massenpunkt zum Zeitpunkt t₀ am Ort x₀
 

Übersichtliche Darstellung der zeitlichen Abhängigkeiten:

Weg-Zeit-Diagramm	Geschwindigkeit-Zeit-Diagramm	Beschleunigungs-Zeit-Diagramm

 

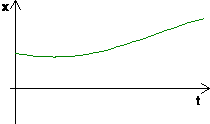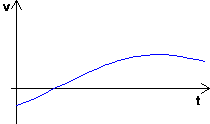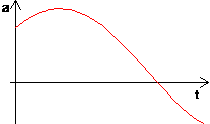a) Gleichförmige Bewegung

Bewegung bei konstanter Geschwindigkeit: v = const    Integration   Interationskonstanten c, d durch Anfangsbedingungen festgelegt, z.B. Ort x0 zum Zeitpunkt t0       Beispiel:

 

b) Gleichförmig beschleunigte Bewegung

Bewegung bei konstanter Beschleunigung: a = const    x (t) ?, v(t) ?  Integration der Gleichungen (s. Definitionen)  Anfangsbedingungen: t0 = 0, x(t0) = x0, v(t0) = v0     x(t) = x0 + v0 t + a t2  v(t) = v0 + a t  a = const   Anwendungen zur "gleichförmig beschleunigten Bewegung":  Bewegung unter dem Einfluß der Erdbeschleunigung (Luftreibung wird vernachlässigt)  Beschleunigung: a = g = konstant = 9.81 m/s2  Beispiel:        Bewegungsgleichungen:  Gleichförmig beschleunigte Bewegung  a = const v(t) = v0 + a× t x(t) = x0 + v0× t + a× t² Unendlich viele Lösungen (Geraden v(t), Parabeln x(t))  Welche Lösungen gilt, hängt von Anfangsbedingungen ab: t(0) = t0, v(t0) = v0, x(t0) = x0    Beispiele:   Lineare Bewegung unter dem Einfluß der Erd-(Fall-)Beschleunigung a = const = g = 9,81  g ist für alle Körper nahe der Erdoberfläche konstant und gleich groß.  Im Folgenden: Reibung vernachlässigt!  Freier Fall:  Koordinatensystem:   Anfangsbedingungen:  t0= 0  x0 = 0  v(0) = 0  a = g                     unabhängig vom fallenden Körper!  Senkrechter Wurf nach oben:  Koordinatensystem:      Anfangsbedingungen:     t0= 0     x0 = 0     v(0) = v0 > 0     a = - g         Steigzeit ts ?  v(ts) = 0    Steighöhe h? Wie lange dauert der ganze Wurf?    v(tl) = - v0  Schiefe Ebene:    Beschleunigung längs der Ebene?    Durch Wahl von  kann Beschleunigung a beliebig zwischen 0 und g eingestellt werden  (sonst: siehe "freier Fall")      Wurf auf schiefer Ebene:      (sonst, siehe "senkrechter Wurf nach oben")

 
 

3.1.3.2 Zweidimensionale Bewegung

Allgemein gilt: 
(für a = const!) 
 

Komponentenzerlegung:	x(t)= ½ ax t2 + v0x t+ x0 ;	vx(t) = ax t + v0x
	y(t)= ½ ay t2 + v0y t+ y0 ;	vy(t) = ay t + v0y
	z(t)= ½ az t2 + v0z t+ z0 ;	vz(t) = az t + v0z

 
a) Beispiel: schräger Wurf (2-dimensional)

Bahnkurve: y (x)?   Einsetzen der Anfangsbedingungen:          x(t) = v0x t                       vx(t) = v0x          y(t)= - ½ g t2 + v0y t         vy(t) = v0y -g t          z(t) = 0  Bewegung in x-Richtung: gleichförmig geradlinig  Bewegung in y-Richtung: gleichförmig beschleunigt    Eliminierung von t  Wurfparabel   Diskussion der Kurve y(x)  Wurfhöhe, Wurfweite, Scheitelpunkt (Übungsaufgabe!)      Beispiel:    Scheitelwert xs:     also: Scheitelwert maximal, wenn Abwurfwinkel = 45° beträgt.