3.3.3 Stirling‘scher Kreisprozess

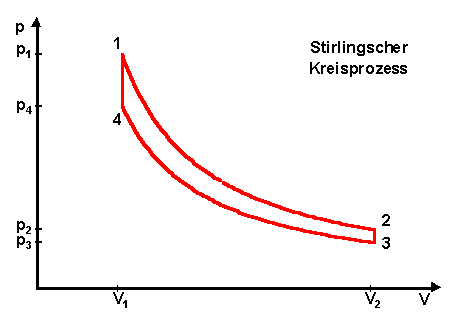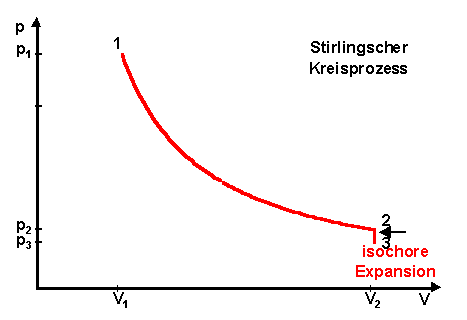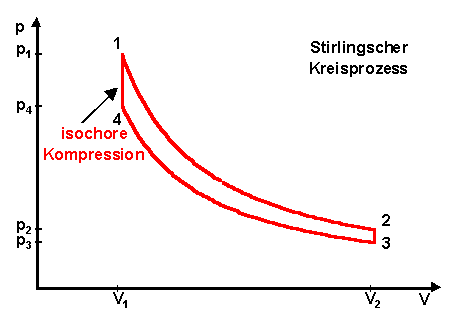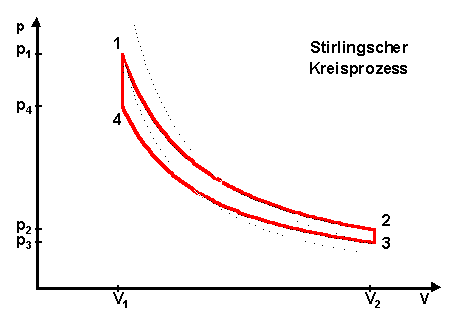
Idealer Stirling'scher Kreisprozess als animiertes Bild zur Verdeutlichung der einzelnen Zustandsänderungen.

Ebenfalls reversibel ist der Stirling‘sche Kreisprozess. Im Folgenden wird ein Stirling-Motor als Wärmekraftmaschine betrachtet.

Teilprozesse des Arbeitszyklus

Im Folgenden werden die einzelnen Teilprozesse des Arbeitszyklus bei einem idealen Stirling‘schen Kreisprozess betrachtet.

a. Isotherme Expansion 1-> 2

Das System wandelt Wärme in Arbeit um (bei konstanter hoher Temperatur T₁) und leistet Arbeit nach außen. Wegen der konstanten Temperatur ändert sich die innere Energie nicht: . Aus dem ersten Hauptsatz folgt

Mit erhält man

(<0, da !).

b. Isochore Abkühlung 2 -> 3

Das System kühlt von hoher Temperatur T₁ auf die niedrige Temperatur T₂ ab, wodurch sich der Druck p verringert. Es wird weder Arbeit verrichtet noch aufgewandt: . Mit dem ersten Hauptsatz folgt

Verwendet man beispielsweise ein zweiatomiges Arbeitsgas (molare Wärmekapazität bei konstantem Volumen ) erhält man

(<0!).

c. Isotherme Kompression 3 -> 4

Das System wandelt von außen zugeführte Arbeit in Wärme bei konstant niedriger Temperatur T₂ um. Die innere Energie ändert sich dabei nicht und man erhält analog zur isothermen Expansion:

(>0, da V₁ < V₂!)

d. Isochore Erwärmung 4 -> 1

Das System wird von der niedrigen Temperatur T₂ auf die höhere Temperatur T₁ erwärmt, wodurch sich der Druck p erhöht. Analog zur isochoren Abkühlung erhält man und

bzw. für ein zweiatomiges Gas

(>0!)

Bilanz der mechanischen Energien und Wärmemengen

Mechanische Energien

Wärmemengen

Das System hat bei der isothermen Expansion die Wärmemenge aufgenommen. Die bei der isochoren Abkühlung abgegebene Wärmemenge wird im Idealfall zwischen gespeichert und dem System bei der isochoren Erwärmung wieder zugeführt . Bei der isothermen Kompression wird die Wärmemenge nach außen abgegeben.

Wirkungsgrad

Für den idealen Wirkungsgrad ergibt sich (T₁>T₂)

Dieser ideale Wirkungsgrad, bei dem Reibungs- und Strahlungsverluste unbeachtet bleiben, ist stets kleiner 1. Das bedeutet, dass nur ein Teil der aufgenommenen Wärmeenergie in mechanische Arbeit umgewandelt wird. Der Rest geht als Abwärme "verloren".

Der Wirkungsgrad ist gleich dem Wirkungsgrad des Carnot Prozesses, da auch der Stirling Prozess vollkommen reversibel ist.