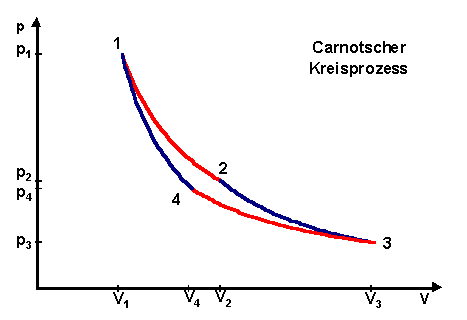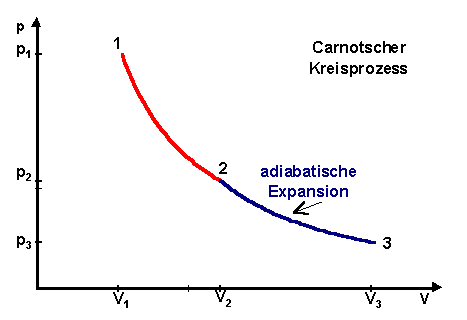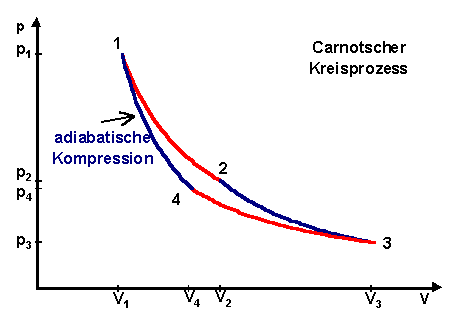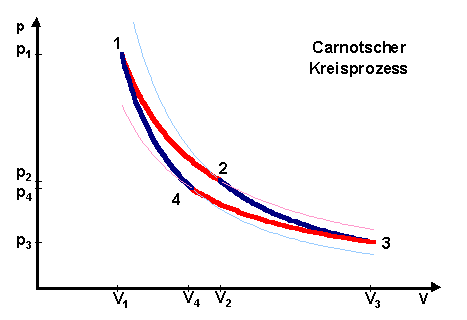
|
 |
| Ein animiertes Bild veranschaulicht die einzelnen Zustandsänderungen bei einem Carnot'schen Kreisprozess. |
Der Carnot’sche Kreisprozess, der im Folgenden behandelt wird, veranschaulicht den zweiten Hauptsatzes. Er realisiert eine reversible Wärmekraftmaschine (Carnot, 1824), die Wärme in Arbeit umwandelt. Umgekehrt können nach dem Carnot-Prozess auch Wärme- bzw. Kältepumpen betrieben werden, die Wärme unter Verrichtung von Arbeit z.B. von einem kalten zu einem warmen Reservoir pumpen (Wärmepumpe). Die Berechnung erfolgt für 1 mol Arbeitsgas.
a. Isotherme Expansion (1 -> 2)
Das System wandelt Wärme vollständig in Arbeit um (bei hoher Temperatur T1) und leistet Arbeit nach außen.
, 
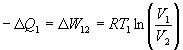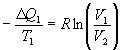
b. Adiabatische Expansion (2 -> 3)
Das System leistet Arbeit nach außen, ohne Zuführung von Wärmeenergie
. Die Energie
für die Arbeit stammt aus der inneren Energie des Arbeitsgases, das sich
abkühlt.
c. Isotherme Kompression (3 -> 4)
Das System gibt Wärme nach außen ab (bei niedriger Temperatur T2) und mechanische Arbeit wird zugeführt.
, 
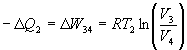Mit Hilfe der Adiabatengleichungen 
(adiabatische Expansion 3 -> 4) und 
(adiabatische Kompression 4 -> 1) erhält man 
und damit
.
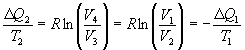d. Adiabatische Kompression (4 -> 1)
Am System wird Arbeit von außen geleistet ohne Abführung von Wärme dQ=0. Die aufgewandte Arbeit wird vollständig zur Erhöhung der inneren Energie verwendet, d.h. das Arbeitsgas erwärmt sich.
Mechanische Energien
Da 
folgt
für die gesamte Arbeit
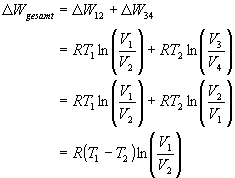
Wärmemengen
Die Wärmemenge 
wurde vom System aufgenommen (bei T1) und 
wurde abgegeben (bei T2).
Der Wirkungsgrad einer Maschine ist definiert als Quotient aus verrichteter mechanischer Arbeit und aufgenommener Wärmeenergie:
Wirkungsgrad.
Für den Wirkungsgrad einer Carnot-Maschine gilt:
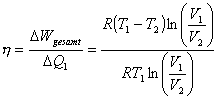
Wirkungsgrad einer Carnot-Maschine
(Achtung:
Temperaturen sind in Kelvin angegeben!)
Der Wirkungsgrad einer Maschine ist immer kleiner 1. Nur ein Teil der aufgenommenen Wärmeenergie kann in mechanische Arbeit verwandelt werden. Der Rest geht als Abwärme "verloren".
Dieser Wirkungsgrad des (reversiblen) Carnot‘schen Kreisprozesses ist der höchste realisierbare Wirkungsgrad!
Zum Beweis12, dass es keine periodisch arbeitende
Maschine mit höherem Wirkungsgrad gibt, betrachte man eine solche Wundermaschine
(mit höherem Wirkungsgrad). Man schaltet nun die Wundermaschine und die
Carnot-Maschine hintereinander, so dass die Carnot-Maschine als Wärmepumpe
funktioniert und die Arbeit von der Wundermaschine erhält, die als Wärmekraftmaschine
arbeitet. Die Maschinen sind so dimensioniert, dass die von der Wundermaschine
pro Umlauf abgegebene Arbeit 
gleich der von der Carnot-Maschine aufgenommenen ist.
Da die Wundermaschine einen höheren Wirkungsgrad als die Carnot-Maschine hat, benötigt sie weniger Wärme als von der Carnot-Maschine dem warmen Reservoir zugeführt wird. Im Widerspruch zum zweiten Hauptsatz würde ohne Energieaufwand Wärme vom kalten zum warmen Reservoir fließen.
Analoge Überlegungen lassen sich für vollkommen reversibel arbeitende Maschinen mit kleinerem Wirkungsgrad anstellen. Daraus folgt:
Alle vollkommen reversibel arbeitenden Maschinen haben gleichen Wirkungsgrad
.
Außerdem bleibt die Entropie bei einem reversiblen Kreisprozess konstant.
12 vgl. Demtröder (1998, Kap. 10.3.5, S. 306)
© Universität Würzburg, Tilo Hemmert 2000
