 |
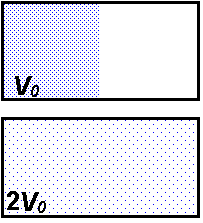
| Zunächst befinden sich alle Gasteilchen in der linken Hälfte des Behälters. Nach der freien Expansion sind sie über den ganzen Behälter verteilt. |
Einen anderen Zugang zur Entropie erschließt die Statistik. Dazu betrachtet
man zum Beispiel die freie Expansion eines Gases vom Volumen ![]() auf
auf ![]() .
.
Wie groß ist nach der Expansion die Wahrscheinlichkeit W10,
dass sich 10 Teilchen wieder in ![]() befinden?
befinden?
![]()
Wie groß ist nach der Expansion die Wahrscheinlichkeit W50,
dass sich 50 Teilchen wieder in ![]() befinden?
befinden?
![]()
Nun verallgemeinern wir die Betrachtung und gehen von der freien Expansion
eines Gases vom Volumen ![]() in ein Volumen
in ein Volumen ![]() aus.
aus.
Die Wahrscheinlichkeit W1, dass sich nach der freien Expansion
wieder alle N Moleküle des Gases im Volumen ![]() befinden und damit der Ausgangszustand wieder hergestellt ist, beträgt
befinden und damit der Ausgangszustand wieder hergestellt ist, beträgt
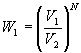 .
.
Im Endzustand müssen sich alle Teilchen im Volumen ![]() aufhalten und die Wahrscheinlichkeit ist damit
aufhalten und die Wahrscheinlichkeit ist damit ![]() .
.
Es gilt nun für das Verhältnis der Ausgangswahrscheinlichkeit W1 und der Wahrscheinlichkeit im Endzustand W2:
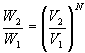
thermodynamisches Wahrscheinlichkeitsverhältnis.17
Um bei Teilchenzahlen von ![]() Zahlen vernünftiger Größenordnung zu erhalten, logarithmiert
man die Gleichung und erhält
Zahlen vernünftiger Größenordnung zu erhalten, logarithmiert
man die Gleichung und erhält
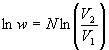 .
.
Mit Hilfe eines reversiblen Ersatzprozesses, bei dem das ideale Gas in einem
Zylinder mit beweglichem Kolben isotherm vom Volumen V1 auf
das Endvolumen V2 entspannt wird, kann die Entropieänderung
berechnet werden. Dazu verwendet man den ersten Hauptsatz ![]() und die Beziehung
und die Beziehung ![]()
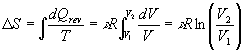 .
.
Dabei bezeichnet ![]() die Stoffmenge, R die allgemeine Gaskonstante.
die Stoffmenge, R die allgemeine Gaskonstante.
Der Vergleich beider Gleichungen zeigt den von Ludwig Boltzmann gefundenen
Zusammenhang zwischen der Änderung der Entropie ![]() und dem thermodynamischen Wahrscheinlichkeitsverhältnis:
und dem thermodynamischen Wahrscheinlichkeitsverhältnis:
![]() .
.
Dabei bezeichnet k den Boltzmann-Faktor. Für die Entropie selbst gilt
![]()
Entropie,
wobei W die Wahrscheinlichkeit angibt, mit der ein thermodynamischer Zustand realisiert ist.
Die Entropie ist ein Maß für die Wahrscheinlichkeit eines Zustands oder den Grad der Unordnung.
Da die Entropie bei allen irreversiblen Zustandsänderungen zunimmt, nimmt der Grad der Unordnung zu.
Weitere Informationen zur Mikroskopischen Betrachtung und zum Zusammenhang zwischen Entropie und Information finden Sie bei der Technischen Universität Braunschweig sowie bei der Universität Ulm.
17 siehe Hering (1992, Kap. 3.3.6.4, S. 185)
© Universität Würzburg, Tilo Hemmert 2000