2.2.4 Boltzmann-Faktor

Aus der barometrischen Höhenformel erhält man

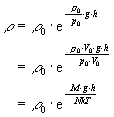
mit der Masse (m: Molekülmasse).

Die Teilchenzahldichte ist abhängig von der Höhe h:

Mit der potenziellen Energie eines Teilchens der Masse m im Gravitationsfeld ergibt sich eine Gleichung, die gleichzeitig die Energieverteilung der Teilchen angibt:

Diese Verteilung lässt sich verallgemeinern:

Dabei geben g₁ bzw. g₂ das statistische Gewicht des Zustandes 1 bzw. 2 an.

Bezeichnungen: kT ist die thermische Energie und

Boltzmann-Faktor

Anwendung

Zwei Zustände

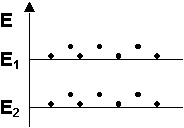Angenommen, es gibt zwei Zustände unterschiedlicher Energien für n Teilchen. Die Teilchen können sich nur in diesen beiden Zuständen aufhalten. Dann gilt für das Verhältnis der Teilchenzahlen n₁ und n₂ in beiden Zuständen im thermodynamischen Gleichgewicht

:
Ist die thermische Energie kT viel größer als die Energiedifferenz der beiden Zustände, dann geht der Boltzmann-Faktor gegen 1 und

:
Ist dagegen die thermische Energie viel kleiner als die Energiedifferenz, so ist der höhere Zustand kaum besetzt und es gilt

Im thermodynamischen Gleichgewicht tritt der Fall nicht auf!

Verallgemeinerung¹⁰

Angenommen, es gibt verschiedene Zustände mit unterschiedlichen Energien E_i. Für die Wahrscheinlichkeit p_i, dass ein Zustand i mit Teilchen besetzt ist, gilt

.

Die Proportionalität gilt nur, wenn alle Energiezustände gleiche Besetzungsmöglichkeiten haben. Andernfalls muss zusätzlich das jeweilige statistische Gewicht g_i der Zustände berücksichtigt werden:

¹⁰  siehe auch Hering (1992, Kap. 3.2.3, S. 154)

© Universität Würzburg, Tilo Hemmert 2000