2.2.5 Maxwell’sche Geschwindigkeitsverteilung

Wir haben bereits festgestellt, dass in einem Gas nicht alle Teilchen die selbe Geschwindigkeit besitzen und haben daher "mittlere Geschwindigkeitsquadrate" verwendet. Wie sind aber nun die Geschwindigkeiten in einem Gas verteilt?

Verteilungsfunktion f(v) zur Herleitung der Maxwell'schen Geschwindigkeitsverteilung.

Zur Beantwortung dieser Frage, nehmen wir an, die Teilchen seien nach einer

f(v)
Verteilungsfunktion

verteilt, die folgende Bedingungen erfüllt:

1. Die Zahl der Teilchen mit Geschwindigkeiten im Intervall von v bis v+dv ist



Dabei ist N die Gesamtzahl der Teilchen und n die Teilchenzahldichte in dem betrachteten Ensemble.

2. Die Verteilungsfunktion ist normiert, d.h.

Wir gehen nach wie vor vom idealen Gas aus, d.h. die Teilchen der Masse m haben kinetische Energie, aber keine Wechselwirkungsenergien.

Zunächst betrachten wir nur die Geschwindigkeitskomponente v_x in x-Richtung. Die Zahl der Teilchen mit einer Geschwindigkeit im Intervall von v_x bis v_x+dv_x ist proportional zum Boltzmann-Faktor:

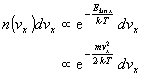
Die Proportionalitätskonstante C

erhält man aus der Normierungsbedingung (und dem Intergral . )

Symmetrische Gaußverteilung f(v) für die Geschwindigkeitskomponente vx.

Damit gilt

Diese Verteilungsfunktion ist eine symmetrische Gaußverteilung.

Nun betrachten wir die Geschwindigkeitskomponenten in allen Raumrichtungen. Die Wahrscheinlichkeit, ein Teilchen mit der Geschwindigkeit zu finden, ist gleich dem Produkt der Einzelwahrscheinlichkeiten:

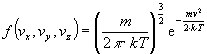
Häufig interessiert man sich nur für den Betrag der Geschwindigkeit , nicht für die Richtung. Die Spitzen aller Geschwindigkeitsvektoren mit Beträgen zwischen v und v+dv spannen eine Kugelschale vom Volumen auf. Daher gilt sich unter der Nebenbedingung für die Integration

Damit erhält man

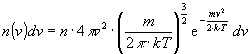
Maxwell’sche Geschwindigkeitsverteilung

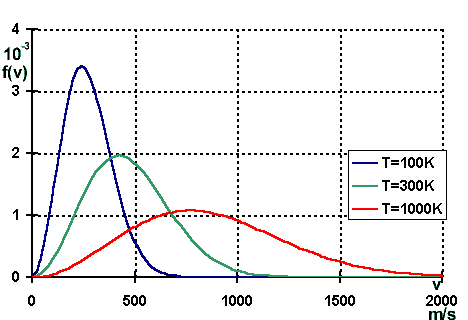Maxwell-Verteilung der Molekülgeschwindigkeiten von Stickstoff bei verschiedenen Temperaturen.

Während eine symmetrische Gaußverteilung ist, ist die Maxwell’sche Geschwindigkeitsverteilung nicht symmetrisch und nimmt ausschließlich positive Werte an!

Die Verteilung der Geschwindigkeiten hängt stark von der Temperatur ab. Wenige Teilchen, die manchmal nicht zu vernachlässigen sind, haben eine sehr hohe kinetische Energie. Daher verdunstet beispielsweise Wasser bei Raumtemperatur oder trocknet gewaschene Wäsche.

© Universität Würzburg, Tilo Hemmert 2000