|
Der Botaniker Robert Brown beobachtet 1827 in flüssigen Lösungen, dass mikroskopisch kleine Teilchen scheinbar ziellose statistische Bewegungen ausführen. Diese Bewegungen haben ihre Ursache in elastischen Stößen der Teilchen mit Flüssigkeitsmolekülen. Im Folgenden wollen wir uns mit der Frage beschäftigen, wie lange die Teilchen eine geradlinige Bewegung ausführen, bevor sie erneut stoßen.
Der Abstand a der Teilchen zum nächsten Nachbarn lässt sich
aus der Teilchenzahldichte 
abschätzen, wobei N die Zahl der Teilchen in einem Volumen V
ist. Unter der Annahme, dass alle Teilchen gleich groß sind, erhält
man für den Abstand der Teilchen 
.
Damit kann der Abstand der Luftmoleküle zum nächsten Nachbarn abgeschätzt
werden:
V=1,0 cm³ Luft hat bei p=1000 hPa und T=273 K 
Teilchen. Damit ergibt sich ein mittlerer Abstand der Teilchen von a=3,3
nm.
 |
|
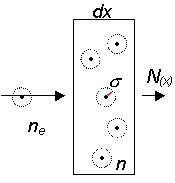
Zur Herleitung der mittleren freien Weglänge. |
  |
Verlust durch Streuung und mittlere freie Weglänge
|
Um nun zur mittleren freien Weglänge zu gelangen, nehmen wir an, dass ein Teilchenstrom entlang der x-Richtung durch ein Streuvolumen A dx fliegt. Mit welcher Wahrscheinlichkeit wird der Teilchenstrom an den anderen Teilchen im Gas gestreut?
An dieser Stelle verlassen wir das Modell des idealen Gases, bei dem wir angenommen
haben, dass die Teilchen ein vernachlässigbar kleines Volumen haben. Zusätzlich
nehmen wir vereinfachend an, dass die Teilchen im Streuvolumen A dx ruhen.
Wir gehen davon aus, dass jeder Stoßpartner einen Stoßquerschnitt
darstellt.
Innerhalb von
werden die einfallenden Teilchen ne gestreut.
Auf der Länge dx stoßen insgesamt 
Teilchen. Dadurch nimmt die Zahl der Teilchen in x-Richtung beim Durchgang durch
das Streuvolumen ab. Für den Verlust durch Streuung ergibt sich:
Nach Integration und Delogarithmieren sieht man, dass die Zahl der Teilchen exponentiell abnimmt:
Man definiert für den Weg, den ein Teilchen im Mittel zurücklegt,
bis es erneut auf einen Stoßpartner trifft, die mittlere Weglänge
d als die Entfernung, nach der der Teilchenstrom auf 
abgefallen ist:
mittlere freie Weglänge
Bei T=273 K und p=1000 hPa errechnet man für die mittlere
Weglänge von Stickstoffmolekülen bei einem Stoßquerschnitt von
:
Vergleiche d=83 nm mit dem vorher berechneten mittleren Abstand a=3,3 nm!
© Universität Würzburg, Tilo Hemmert 2000