5.1 Zustandsgleichung realer Gase
(van-der-Waals-Gleichung)

In der kinetischen Gastheorie wurde das Modell des idealen Gases zu Grunde gelegt, das von punktförmigen Teilchen ohne gegenseitige Wechselwirkung ausgeht. Wie ändert sich die Zustandsgleichung, wenn wir stattdessen reale Gase betrachten?

Bei realen Gasen sind im Gegensatz zu idealen Gasen zusätzlich zu beachten:

1. Eigenvolumen der Teilchen
2. (Anziehende) Kräfte zwischen Teilchen

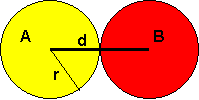Demonstration des Kovolumens: Zwei Teilchen können sich nicht näher kommen als 2r.

Das Eigenvolumen der Teilchen kann bei sehr hohen Drücken nicht mehr gegenüber dem Volumen V vernachlässigt werden, das dem Gas zu Verfügung steht. Zwei Teilchen (betrachtet als starre Kugeln mit Radius r) können sich nie näher kommen als d=2r. Weitere Überlegungen zeigen, dass von dem Volumen V, das einem idealen Gas mit punktförmigen Teilchen zur Verfügung stünde, das vierfache Eigenvolumen V_a der N Atome abgezogen werden muss:

Kovolumen.

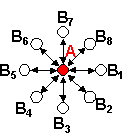Demonstration des Binnendrucks: Im Inneren eines Gases heben sich Kräfte auf ein Teilchen auf.

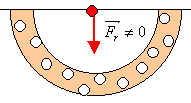An der begrenzenden Wand / Oberfläche wirkt eine resultierende Kraft nach innen.

Die anziehenden Kräfte zwischen den Teilchen (ihre potenzielle Energie) können bei tiefen Temperaturen bzw. großen Dichten nicht mehr vernachlässigt werden und führen zur Korrektur des Drucks p. Während es im Inneren eines Gases keine resultierende Kraft gibt, resultiert auf ein Teilchen an einer Grenzflächen (Flüssigkeit – Gas, Gas – feste Wand) eine Kraft proportional zur Zahl der anziehenden Teilchen und damit zur Dichte der Substanz. Die von der Oberfläche nach innen gerichtete Gesamtkraft auf alle Teilchen an der Oberfläche ist proportional zur Teilchenzahldichte n und somit proportional zum Quadrat der Dichte: Sie verursacht einen Druck, der abhängig vom Material ist (Materialkonstante a):

Binnendruck.

Unter Berücksichtigung des Eigenvolumens und des Binnendrucks modifiziert sich die allgemeine Gasgleichung für 1 mol

van-der-Waals-Gleichung.

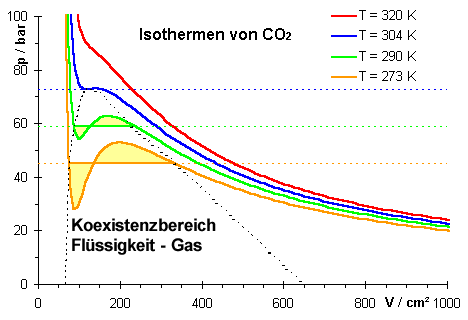Isothermen eines realen Gases werden durch die van-der-Waals-Gleichung beschrieben.

Der Verlauf von Isothermen (T=const) in einem p(V)-Diagramm hängt von der Art des verwendeten Gases ab (Stoffkonstanten a, b in der van-der-Waals-Gleichung).

Weit oberhalb der sogenannten kritischen Temperatur T_k erhält man näherungsweise Isothermen des idealen Gases.

Unterhalb der kritischen Temperatur beobachtet man, dass für große Volumina Isothermen näherungsweise denen eines idealen Gases entsprechen. Nach einem Phasenübergang vom gasförmigen in den flüssigen Zustand sieht man, dass bei kleinen Volumina der Druck p mit abnehmendem Volumen stark ansteigt.

Im Koexistenzgebiet (flüssig – gasförmig) verlaufen Isothermen als Maxwell-Geraden. Der experimentell messbare Verlauf der Isothermen entspricht nicht mehr der van-der-Waals-Gleichung. Die Modellannahmen (für Gas) stimmen im Koexistenzbereich Flüssigkeit – Gas nicht mehr.

© Universität Würzburg, Tilo Hemmert 2000