|
 |
| Isothermen eines realen Gases werden durch die van-der-Waals-Gleichung beschrieben. |
Die van-der-Waals-Isotherme hat am kritischen Punkt einen Sattelpunkt im p(V)-Diagramm,
den man einfach berechnet, indem man erste und zweite Ableitung nach dem Volumen
gleich Null setzt: 
und 
Damit erhält man für die Stoffkonstanten in der van-der-Waals-Gleichung:
Über die Bestimmung der kritischen Größen 
lassen sich somit Aussagen bezüglich des Eigenvolumens der Teilchen und
der Anziehungskräfte zwischen den Teilchen treffen.
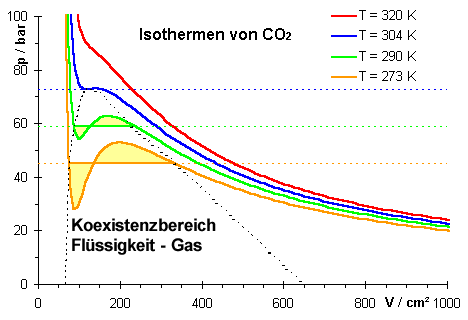
Wir haben gesehen, dass der kritische Punkt im p(V)-Diagramm den Wendepunkt der Isothermen bei der kritischen Temperatur Tk markiert. Im p(T)-Diagramm ist er der Endpunkt der Dampfdruckkurve, d.h. der Koexistenz von Flüssigkeit und Gas. Oberhalb der kritischen Temperatur gibt es keine flüssige Phase mehr.
Experiment: Verflüssigung von Schwefelhexafluorid
Experiment: Verdampfen von Chlorpentanfluoräthan
© Universität Würzburg, Tilo Hemmert 2000