Laminare Rohrströmung
Der Mensch besitzt ein Netz von Blutgefäßen. Wir setzen uns nun mit der Frage auseinander,
welches Volumen
V einer Flüssigkeit in der Zeit
t durch ein solches Netz strömt
und von welchen Parametern dieser Wert beinflusst wird.
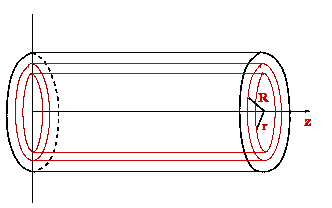
Dazu nehmen wir an, dass eine Ader ein zylindrisches Rohr mit kreisför-migen Querschnitt vom
Radius
R darstellt. Innerhalb dieses mit Flüssigkeit gefüllten Rohres herrscht ein
Druckunterschied
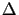 p = p1 - p2 zwischen den Ebenen
z = 0 und
z = l (vgl. Abb. ). Ein im Inneren
gelegener, konzentrischer Flüssigkeitszylinder der Länge
l und Radius
r wird jetzt
näher betrachtet. Der Betrag der Druckkraft
F
p = p1 - p2 zwischen den Ebenen
z = 0 und
z = l (vgl. Abb. ). Ein im Inneren
gelegener, konzentrischer Flüssigkeitszylinder der Länge
l und Radius
r wird jetzt
näher betrachtet. Der Betrag der Druckkraft
F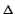 p muss im stationären Fall
gleich dem der Reibungskraft
FR sein, die auf die
Zylinderoberfläche wirkt,
p muss im stationären Fall
gleich dem der Reibungskraft
FR sein, die auf die
Zylinderoberfläche wirkt,
Als Reibungskraft wurde die
Formel für Viskosität
mit der Stirnfläche des Hohlzylinders
A = 2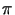 r l benutzt. Löst man die obige
Gleichung nach
v auf und integriert danach beide Seiten, beachtet die Randbedingung
v(R) = 0 (Fluid haftet am Rand des Rohres
und bewegt sich deswegen nicht), ergibt sich folgendes Geschwindigkeitsprofil:
r l benutzt. Löst man die obige
Gleichung nach
v auf und integriert danach beide Seiten, beachtet die Randbedingung
v(R) = 0 (Fluid haftet am Rand des Rohres
und bewegt sich deswegen nicht), ergibt sich folgendes Geschwindigkeitsprofil:
Wie wir erkennen, handelt es sich um eine parabolische Geschwindigkeitsverteilung,
d. h. die Geschwindigkeit
v(r) bildet räumlich betrachtet ein Rotationsparaboloid. Nun können wir
die Flüssigkeitsmenge
V berechnen, die in der Zeit
t durch das Rohr fließt.
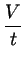 |
= |
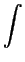 v(r) dA v(r) dA |
|
| |
= |
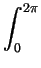 d d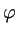 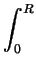 r dr v(r) r dr v(r) |
|
| |
= |
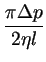 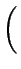 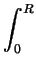 R2r dr - R2r dr - 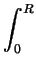 r3 dr r3 dr |
|
| |
|
|
|
| |
= |
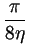 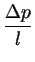 R4. R4. |
|
Den Quotienten aus Volumen
V und der Zeit
t nennt man Stromstärke
I. Damit gilt
Diese Formel wird als Hagen2.1-Poiseuille2.2-Gesetz bezeichnet . Ein Beispiel hierzu sind die Blutgefäße des Menschen. Durch die
R4-Abhängigkeit bewirken bereits minimale Ablagerungen in
Blutgefäßen, dass der Blutdruck steigen muss, wenn der Blutstrom konstant gehalten
werden soll.
Universität Würzburg
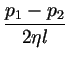 r dr
r dr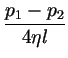 (R2 - r2).
(R2 - r2).