Navier-Stokes-Gleichung
Bei der Behandlung idealer Fluide
früher sind wir davon ausgegangen, dass lediglich Druck- und Schwerkraft wirken. Im Fall realer
Fluide ist klar, dass zusätzlich noch die bereits beschriebene Reibungskraft
auf eine Flüssigkeit wirken
muss. Die Gesamtkraft
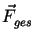 ist also:
Es gilt :
ist also:
Es gilt :
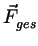 |
= |
 m m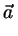 |
|
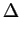 m m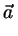 |
= |
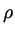 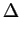 V V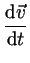 |
|
| |
= |
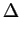 m m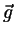 - gradp - gradp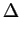 V + V + 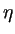  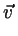 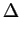 V V |
|
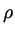 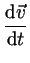 |
= |
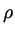 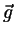 - gradp + - gradp + 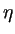  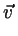 |
|
Mit dieser Bewegungsgleichung, der sogenannten Navier2.4-Stokes-Gleichung, lässt sich die
ganze klassische Hydrodynamik beschreiben . Sie enthält im Unterschied zur
Euler-Gleichung den Term
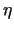
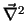
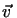
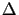 V. Er berücksichtigt die innere Reibung im Fluid.
V. Er berücksichtigt die innere Reibung im Fluid.
Die Navier-Stokes-Formel ist eine nichtlineare
partielle Differentialgleichung. Ihre Lösung gibt die Geschwindigkeitsverteilung in einer
Flüssigkeit als Funktion von Ort und Zeit (
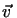 = f (
= f (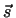 , t)) an. Allerdings kennt die
Mathematik noch keine Möglichkeiten, die Gleichung analytisch zu lösen (außer
per Zufall).
, t)) an. Allerdings kennt die
Mathematik noch keine Möglichkeiten, die Gleichung analytisch zu lösen (außer
per Zufall).
Universität Würzburg
![]() = f (
= f (![]() , t)) an. Allerdings kennt die
Mathematik noch keine Möglichkeiten, die Gleichung analytisch zu lösen (außer
per Zufall).
, t)) an. Allerdings kennt die
Mathematik noch keine Möglichkeiten, die Gleichung analytisch zu lösen (außer
per Zufall).