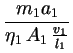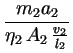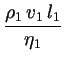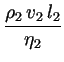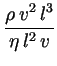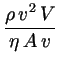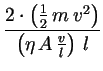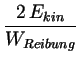Die Reynoldszahl
Wenn wir die Gewichtskraft vernachlässigen, greifen in der Regel nur
Druckkräfte, Reibungskräfte
FR und Trägheitskräfte
FT an Fluidelementen und
umströmten Körpern an. Diese müssen in allen Punkten der Strömung im Gleichgewicht sein. Ist das Verhältnis von Reibungs- und
Trägheitskraft in ähnlichen Punkten
P1 und
P2 gleich, dann liegen auch
ähnliche Strömungen vor (vgl. Abb. ).
Abbildung:
Ähnliche Strömungen um verschiedene Zylinder
 |
Mathematisch ausgedrückt:
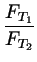
=
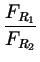
.
Die Reibung
tritt dabei zwischen den Flüssigkeitsschichten auf und berechnet sich aus
FR = 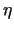 A
A 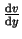 . Als Trägheitskraft setzen wir allgemein
FT = ma an. Die Länge
l ist die einzige formbezogene Größe. Durch sie gehen Eigenschaften des durch- bzw. umströmten
Körpers ein (z. B. der Durchmesser eines Rohres).
Verwenden
wir die bekannten Beziehungen
. Als Trägheitskraft setzen wir allgemein
FT = ma an. Die Länge
l ist die einzige formbezogene Größe. Durch sie gehen Eigenschaften des durch- bzw. umströmten
Körpers ein (z. B. der Durchmesser eines Rohres).
Verwenden
wir die bekannten Beziehungen
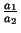 =
= 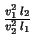 ,
,
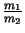 =
= 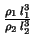 und
und
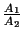 =
= 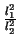 , dann gilt :
, dann gilt :
Was sagt uns diese Gleichung?
Um zwei Strömungen ähnlich zu nennen, muss der Quotient
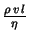 für beide ungefähr gleich sein . Man nennt diese dimensionslose Größe
Reynoldszahl3.1
Re,
Ihre physikalische Bedeutung wird klar, wenn sie mit dem Produkt
l2 . v
erweitert wird:
für beide ungefähr gleich sein . Man nennt diese dimensionslose Größe
Reynoldszahl3.1
Re,
Ihre physikalische Bedeutung wird klar, wenn sie mit dem Produkt
l2 . v
erweitert wird:
Die Reynoldszahl spiegelt also das Verhältnis zwischen doppelter
Bewegungsenergie eines Volumens
V, das sich mit der Geschwindigkeit
v bewegt und der
Reibungsarbeit, die geleistet wird, wenn sich das Volumenelement um seinen Durchmesser
l
bewegt. Die sogenannte kritische Reynoldszahl
Rekrit hängt ab von der Viskosität
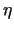 , der Strömungsgeschwindigkeit
v des
Fluids und der Geometrie der Flussführung. Ist die Reynoldszahl eines Stroms kleiner
als
Rekrit, fließt er laminar. Bei Werten oberhalb als
Rekrit liegt turbulente
Strömung vor. In der folgenden Tabelle sind einige kritische Reynoldszahlen angegeben
.
, der Strömungsgeschwindigkeit
v des
Fluids und der Geometrie der Flussführung. Ist die Reynoldszahl eines Stroms kleiner
als
Rekrit, fließt er laminar. Bei Werten oberhalb als
Rekrit liegt turbulente
Strömung vor. In der folgenden Tabelle sind einige kritische Reynoldszahlen angegeben
.
|
in Luft |
Re |
in Wasser |
Re |
|
Auto |
107 |
Schiff |
107 bis
1010 |
|
Verkehrsflugzeug |
109 |
kleiner Fisch |
105 |
|
kleiner Vogel |
2 . 107 |
Delphin |
107 |
Universität Würzburg

![]() =
= ![]() ,
,
![]() =
= ![]() und
und
![]() =
= ![]() , dann gilt :
, dann gilt :