Dichtebeständige Fluide

Wir betrachten im Folgenden die stationäre Strömung eines dichtebeständigen (d. h.  inkompressiblen) Fluids (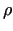 = konstant). Das Fluid fließt in einer Stromröhre mit wechselndem Querschnitt (z. B. ein teilweise verengtes Blutgefäß eines Menschen).
Bei stationärer Strömung bleibt die Geschwindigkeit 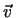an jedem Ort zeitunabhängig ( 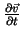= 0). Die Strömungsgeschwindigkeit kann sich aber in Abhängigkeit vom Ort 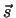ändern.

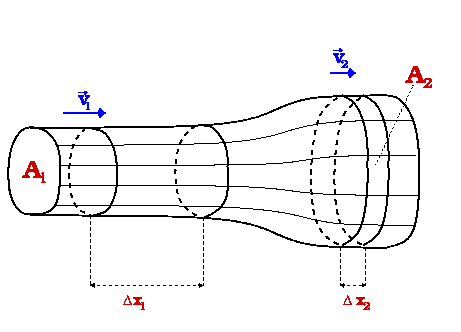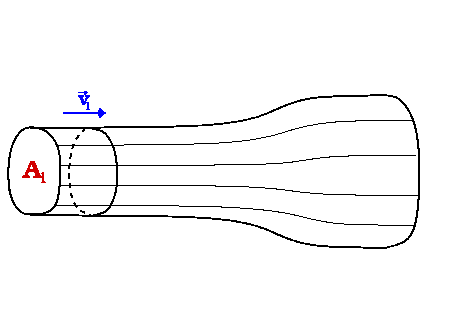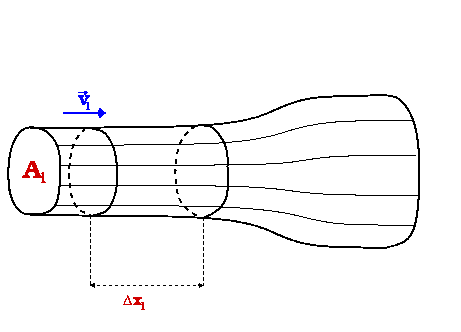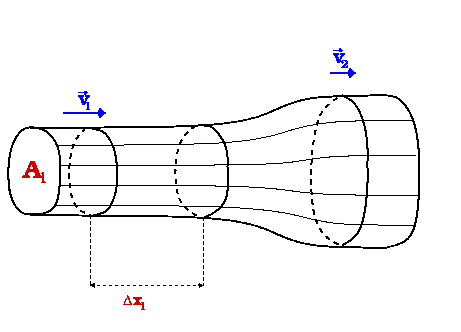
Abschnitte eines Strömungsfeldes (vgl. Bild ) bezeichnet man als homogen, wenn alle Stromfäden parallel zueinander verlaufen. In diesen Rohrabschnitten hat die Strömung gleiche Geschwindigkeit (solange sich die Querschnittsfläche der Stromröhre nicht ändert). Da das Fluid dichtebeständig ist, muss durch jeden Querschnitt A einer Stromröhre im Zeitabschnitt 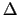t das gleiche Fluidvolumen strömen .
Dies bedeutet (unter Verwendung des vektoriellen Betrags der Geschwindigkeit):

V₁ = A₁x₁ = A₁v₁t,

V₂ = A₂x₂ = A₂v₂t.

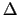Aus V₁ = 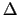V₂ ergibt sich:

Dieser Zusammenhang wird als Kontinuitätsgleichung für dichtebeständige Fluide bezeichnet. Die Strömungsgeschwindigkeit v muss steigen, wenn der Flächenquerschnitt sinkt.

Umgeformt macht die Kontinuitätsgleichung deutlich, dass sich die Strömungsgeschwindigkeiten v_i umgekehrt proportional zu den Querschnitten A_i der Strömungsröhre verhalten.

= .

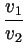
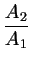
Nachfolgende Abb. zeigt eine Realisierung der beschriebenen Kontinuitätsgleichung. Die Veränderung von Strömungsgeschwindigkeit und Fläche ist im Video deutlich erkennbar.

Abbildung: Veranschaulichung der Kontinuitätsgleichung; (Video 1,4 MB oder Video 1,0 MB)