Bernoulli-Gleichung (Energiesatz)
Wir beschäftigen uns im folgenden Abschnitt mit idealen Flüssigkeiten, die
stationär (
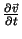 = 0) und inkompressibel
(
= 0) und inkompressibel
(
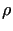 = konstant) sind. Außerdem wirkt die Schwerkraft
auf das Medium.
= konstant) sind. Außerdem wirkt die Schwerkraft
auf das Medium.
Abbildung:
Energiebilanz
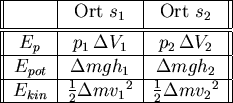 |
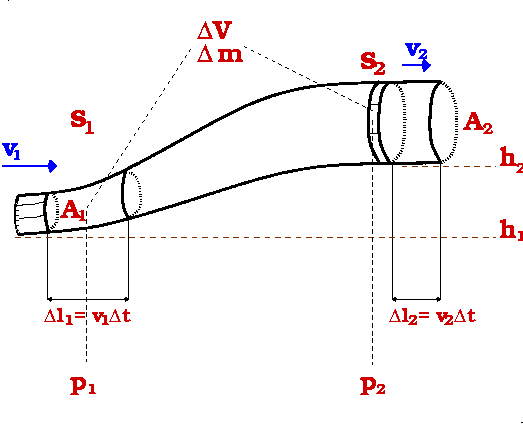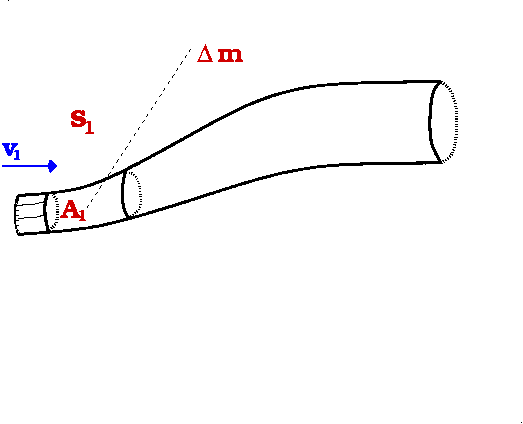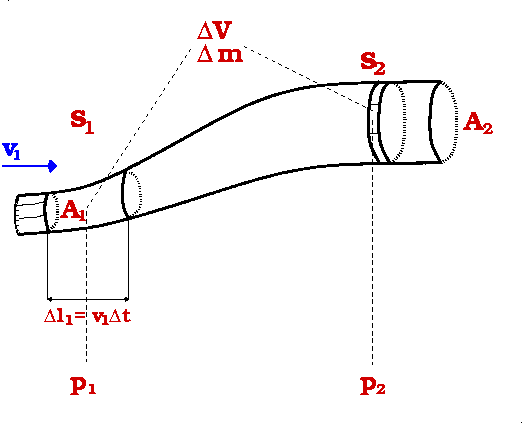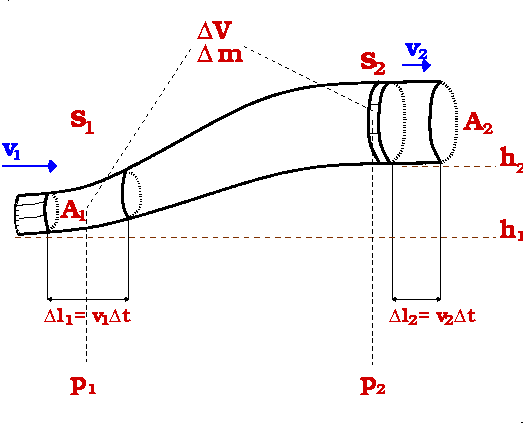
Die Flüssigkeit soll durch ein Rohr (vgl. Bild 3.5) mit veränderlichem Querschnitt
A und
variierender Höhe
h fließen. Am Ort
s1 wird das Volumenelement
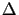 V1 durch den Querschnitt
A1 mit der Geschwindigkeit
V1 durch den Querschnitt
A1 mit der Geschwindigkeit
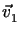 bewegt. Da die
Dichte des Fluids als konstant angenommen wird, gilt mit der
Kontinuitätsgleichung
die Massenerhaltung, d. h. dass in der Zeit
bewegt. Da die
Dichte des Fluids als konstant angenommen wird, gilt mit der
Kontinuitätsgleichung
die Massenerhaltung, d. h. dass in der Zeit
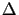 t am Ort
s2
genausoviel Masse
t am Ort
s2
genausoviel Masse
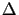 m aus dem Querschnitt
A2 herausströmt, wie bei
A1
hineinströmt. Es gilt also:
woraus folgt:
Nun betrachten wir die geleistete Druckarbeit
Wp an den Orten
si näher. Zunächst ist klar, dass eine Druckdifferenz
p1 - p2
m aus dem Querschnitt
A2 herausströmt, wie bei
A1
hineinströmt. Es gilt also:
woraus folgt:
Nun betrachten wir die geleistete Druckarbeit
Wp an den Orten
si näher. Zunächst ist klar, dass eine Druckdifferenz
p1 - p2 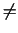 0
aufgrund der verschienden Geschwindigkeiten
0
aufgrund der verschienden Geschwindigkeiten
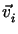 vorhanden
sein muss. Im engen Teil der Röhre (Ort
s1) leistet die Druckkraft
F1 die Arbeit:
vorhanden
sein muss. Im engen Teil der Röhre (Ort
s1) leistet die Druckkraft
F1 die Arbeit:
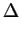 W1
W1 =
F1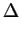 l1
l1 =
p1A1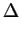 l1
l1 =
p1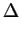 V1
V1.
Im breiten Teil der Röhre (Ort
s2) wird die Arbeit
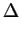 W2
W2 =
F2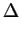 l2
l2 =
p2A2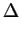 l2
l2 =
p2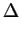 V2
V2
gegen die Druckkraft geleistet. Die hieraus resultierende Druckenergieänderung
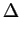 Ep Ep |
= |
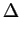 W1 - W1 - 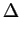 W2 W2 |
|
| |
= |
p1 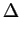 V1 - p2 V1 - p2 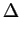 V2 V2 |
|
| |
= |
(p1 - p2) 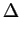 V V |
|
muss identisch
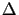 E (Differenz aus
kinetischer Energie
Ekin und potentieller Energie
Epot an den Orten
si)
sein. Am Ort
s1 besitzt die Flüssigkeit mit der Masse
E (Differenz aus
kinetischer Energie
Ekin und potentieller Energie
Epot an den Orten
si)
sein. Am Ort
s1 besitzt die Flüssigkeit mit der Masse
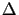 m im Fluidelement
m im Fluidelement
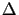 V die Energie
V die Energie
E1 =
Ekin1 +
Epot1 =
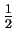
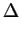 mv12
mv12 +
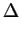 mgh1
mgh1.
Für den Ort
s2 gilt:
E2 =
Ekin2 +
Epot2 =
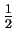
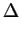 mv22
mv22 +
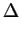 mgh2
mgh2.
Wir erhalten für
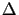 E:
E:
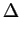 E E |
= |
E2 - E1 |
|
| |
= |
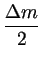 (v22 - v12) + (v22 - v12) + 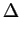 mg(h2 - h1). mg(h2 - h1). |
|
Wie zuvor erläutert können wir
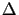 Ep und
Ep und
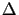 E gleichsetzen:
E gleichsetzen:
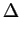 Ep Ep |
= |
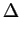 E, E, |
|
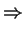 (p1 - p2) (p1 - p2) 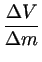 |
= |
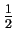 (v22 - v12) + g (h2 - h1). (v22 - v12) + g (h2 - h1). |
|
Damit ergibt sich
Diese Gleichung für reibungsfreie, stationäre, inkompressible Flüssigkeiten nennt man
Bernoulli1.2-Gleichung . Sie folgt aus der Energieerhaltung. Die Gesamtenergie als Summe aus Druckenergie,
potentieller Energie und kinetischer Energie bleibt entlang der Röhre
konstant.
Eine besonders eindrucksvolle Anwendung der
 Bernoulli-Gleichung
ist das
sogenannte
Bernoulli-Gleichung
ist das
sogenannte
 Hydrodynamische Paradoxon.
Hydrodynamische Paradoxon.
Kennen Sie
 Lord Rayleigh?
Lord Rayleigh?
Die Grösse
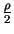 v2 = pd bezeichnet man als
v2 = pd bezeichnet man als
 dynamischen Druck.
dynamischen Druck.
Die Differenz aus Gesamtdruck
p und dynamischen Druck
pd nennt man
 statischen Druck
ps.
statischen Druck
ps.
 Was passiert bei horizontalen Strömungen?
Was passiert bei horizontalen Strömungen?
Universität Würzburg
![]() Bernoulli-Gleichung
ist das
sogenannte
Bernoulli-Gleichung
ist das
sogenannte
![]() Hydrodynamische Paradoxon.
Hydrodynamische Paradoxon.
![]() Lord Rayleigh?
Lord Rayleigh?
![]() v2 = pd bezeichnet man als
v2 = pd bezeichnet man als
![]() dynamischen Druck.
dynamischen Druck.
![]() statischen Druck
ps.
statischen Druck
ps.
![]() Was passiert bei horizontalen Strömungen?
Was passiert bei horizontalen Strömungen?