Fluide mit variierender Dichte

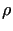
Im Gegensatz zum vorherigen Abschnitt (vgl. Dichtebeständige Fluide) beschäftigen wir uns nun mit nicht dichtebeständigen Fluiden ( 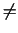konstant). Dazu betrachten wir ein beliebiges Volumen V eines Fluids. Es hat die Masse:

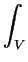
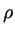
M =  dV.

In nebenstehender Abbildung wird ein Oberflächenelement d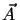 des Volumens V mit der Oberfläche A dargestellt. Der Betrag | d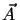| entspricht genau dem Flächeninhalt des Elements d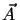. Das Oberflächenelement d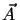 zeigt in Richtung der äußeren Flächennormalen. Wie groß ist die Masse M, die durch dieses Oberflächenelement in der Zeit dt geflossen ist?

In der Zeit dt legt die Flüssigkeit den Weg d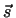 =  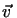dt zurück. Also gilt für die Masse dM, die in der Zeit dt durch das Oberflächenelement geflossen ist:

dM = - dt  od.

In der Formel wird das Skalarprodukt durch o verdeutlicht. Wenn Masse aus dem Volumen V ausströmt ist dM negativ. Integriert man noch über alle Oberflächenelemente von A, erhält man als Massenänderung des Volumens V im Zeitraum dt folgendes Ergebnis:

dM = - dt od.

Diese Massenänderung kann man auch durch die zeitliche Änderung der Dichte 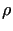(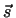, t) im Volumen V darstellen:

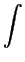
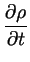
dM = + dt dV.

Strömt Masse in ein Volumen hinein, so ist dM positiv. Wir haben zwei Ansätze für die Berechnung der Massenänderung dM gefunden. Setzt man beide gleich:

-  od =  dV

und wendet den Satz von Gauß an,

 od = div() dV,

erhält man:

( + div()) dV = 0.

Damit diese Gleichung den Wert Null annimmt, reicht es zu fordern:

Diese Formel stellt die allgemeine Kontinuitätsgleichung dar. Man bezeichnet sie auch als Massenerhaltungssatz .
Wie hängen jetzt alle Erkenntisse zusammen?

Beispielaufgaben zum Thema findet man hier (externer Link).